Как мы уже писали в статье «Линейные газовые вихри», тело газового вихря может подвергаться сжатию окружающей средой в процессе образования самого вихря. Подтверждением этому служит следующий факт, что тело смерча имеет тонкое сечение по сравнению с его основанием, так как трение о поверхность земли или воды не позволяет вихрю развить сильную скорость вращения. Существует и другое подтверждение сжатия тела вихря, например, при запуске турбореактивного двигателя в самолете – перед воздухозаборником часто образуется вихрь, у которого площадь поперечника в сотни раз меньше площади поперечного сечения самого воздухозаборника. Также экспериментальным путем доказано, что поступление воздуха в воздухозаборник турбореактивного двигателя самолета вне вихря полностью отсутствует. Скоростные характеристики продольного течения в самом вихре имеют высокие значения, практически весь воздух, поступающий в турбину, проходит через вихрь, который появляется произвольно на входе в компрессор.

Поэтому отрицать факт самопроизвольного уменьшения площади поперечного сечения вихря не имеет смысла, так как данный факт подтвержден в ходе экспериментальных исследований. Уменьшение площади поперечного сечения вихря является результатом уменьшения его радиуса. Поэтому формирование вихря сопровождается уменьшением радиуса с параллельным уплотнением тела самого вихря.

Существует несколько видов вращательного движения тела с переменным радиусом. Современная механика рассматривает данный вопрос не совсем объективно.

Одним из видов вращательного движения – это самопроизвольное вращательное движение тела, без подвода энергии, что представлено на рисунке ниже.

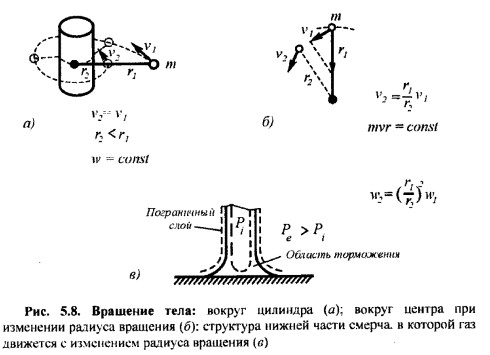
Движение тела производится вокруг цилиндра, на который намотана нить, удерживающая тело. В данном случае тело движется инерционно вокруг цилиндра, осуществляя вращение вокруг мгновенного центра вращения, который находится на образующей цилиндра (на рисунке представлена в точке О). Мгновенный центр вращения перемещается вслед за телом. Нить имеет натяжение, траектория движения тела в определенный момент времени строго перпендикулярна удерживающей нити. В данном случае проекция силы натяжения нити приравнивается к нулю.

При меняющемся (уменьшающемся) радиусе тангенциальное ускорение отсутствует, так как тело движется с постоянной линейной скоростью, при этом потери отсутствуют. Поэтому r=var, а линейная скорость, количество движений и энергия будут постоянными:

V=const; p=mv=const; w=mv2/2=const.

Такие условия могут соответствовать движению при отсутствии потерь и подводе энергии.

Второй вид движения тела с переменным радиусом – это движение тела вокруг неподвижного центра вращения при изменении радиуса за счет присутствия энергии извне (пример такого движения показан на рисунке, приведенном ниже).

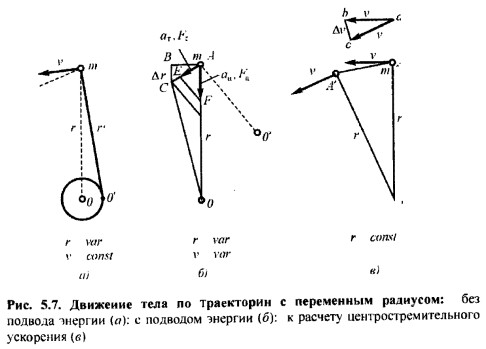
В данном случае, для того чтобы уменьшить радиус траектории, необходимо произвести дополнительную работу по преодолению сопротивляющейся центробежной силы. Тогда тело начнет движение по спиральной траектории, при этом угол между нитью, удерживающей тело, и траекторией будет меньше прямого угла. В данной схеме движения присутствует проекция центробежной силы на траекторию. Общее же движение массы происходит по кривой, мгновенным центром вращения для данного движения будет точка О', которая удалена в сторону от точки О и к ней прикреплена нить к которой направлена сила Fц (проекция силы Fц не приравнивается к нулю). В данном случае тело приобретает ускорение вдоль траектории движения.

Если рассматривать обычное вращательное движение по подобию треугольника АА'О и abc, то можно увидеть следующее:

Δv/v=S/r=vΔt/r

Или

Δv/Δt=αц=v2/r;

Если взглянуть на подобие треугольника АВС и AEF, то становится ясным, что:

at/aц=-vr/vt

или

ar=-aц(vr/vt)=-(vt2vr/rvt)=vtvr/r

имеем

ar=-ωvr

в данном случае ускорение массы имеет природу ускорения Кориолиса.

Перемножив два члена уравнения на радиус r, мы получаем

arr+vrvt=0

при интегрировании по времени, получается следующее выражение

∫(arr+vrvt)dt=∫((∂vt/∂t)r+vt(∂r/∂t))dt=const

Так как в скобках присутствует полный дифференциал, то мы получаем

vr=const

если масса тела постоянна, то mvr=const

отсюда вытекает, при условии r2p1=mv1, где w2=mv22/2>w1=mv12/2

Из данных выражений мы видим, что закон постоянства момента количества движения будет справедливым, если в системе будут происходить изменения энергии за счет внешних источников, которые направлены на определенные изменения, то есть на изменение радиуса вращения тела. Данный случай имеет принципиальное отличие от ранее рассматриваемых тем, которые касались изменения энергии вращения. В данном случае другие характеристики, влияющие на ускорение, к примеру, температура, были неизменными.

В этом примере тангенциальная скорость движения тела при уменьшении радиуса вращения будет намного большей, чем первоначальное ее значение, и будет определяться следующим выражением, которое получено из условия постоянного момента количества движения:

uk=(ro/rk)uo

Такое условие должно соблюдаться и при формировании вихревого движения, то есть чем больше сжимается вихрь, тем больше скорость движения потока воздуха по продольной траектории внутри этого самого вихря. Такое условие должно присутствовать и в структуре уже сформированного вихря, в котором внутренние слои имеют большую скорость движения, чем внешние слои.

Энергия тангенциального движения, которая приобретается массой в определенный период времени, будет равна

wr=FtΔSt/Δt=matvt=m(vt2vr/r)=mωvrvt=mω2vrr

Энергия, потраченная на радиальное перемещение тела за тот же промежуток времени, будет иметь следующее выражение

wц=FцΔS/Δt=maц vц=m(vr2 vt/r)

отсюда следует, что

wr=wц

это доказывает, что приобретенная массой энергия имеет только внешнее происхождение.

Сила, которая ускоряет массу, равна

Fr=vt vr/r=mωvr

и будет пропорциональна угловой скорости и скорости изменения величины радиуса.

Сила, что приложена к массе в радиальном направлении имеет следующее значение:

Fr=vr2/r=mω2r

Fr- это полная сила, на которую действует энергия, пытающаяся преодолеть ее при перемещении тела со скоростью vr. Поэтому данная энергия является основной, так как за счет ее обеспечивается сокращение радиуса и происходит приобретение дополнительной энергии вращения тела.

Рассматривая схему накопления энергии вращающимся телом, становится ясным, что формирование газовых вихрей весьма энергоемкое образование.

Такой вывод актуален не только в примерах вращения твердых тел, но и для несжимаемых жидкостей, когда энергия радиального движения используется на изменение радиуса вращения и на изменение энергии тангенциального движения. В случае с сжимаемым газом энергия расходуется еще и на изменение внутренней энергии газа, так как происходит его сжатие.

Общая же картина имеет более сложную структуру.

В случае рассмотрения некоторого объема газа во время образования вихря, который может сжиматься без изменения структурных характеристик, то в данном объеме может происходить неизбежное увеличение давления газа, так как действует известный закон

P=RT/V

Где R является универсальной газовой постоянной, Т – абсолютная температура, а V – объем. Но при таких условиях о формировании самого вихря не может быть и речи. Известно, что при формировании вихря разные слои находятся на различных расстояниях от центра вихря, что приводит к тому, что их скоростные характеристики отличаются друг от друга. Внутренние слои движутся быстрее, чем наружные. Поэтому можно с уверенностью сказать, что в каждой точке вихря присутствует градиент скорости, что в целом меняет картину.

Давайте рассмотрим дифференциальную формулу Бернулли

pvdv+dP=0,

которая свидетельствует об увеличении скорости потока и снижении давления.

При снижении давления в газовом потоке будет происходить снижение температуры и компенсация добавлением массы газа со стороны. Поэтому в стенках тела газового вихря присутствует повышенная плотность и низкая температура, что выглядит более реалистично.

Необходимо отметить, что приведенные нами соображения не являются строгими, так как сжатие тела газового вихря происходит в результате работы давления внешнего относительно тела самого вихря, состоящего из газа. Данное давление способно разгонять потоки газа, и таким образом, ускорение потока происходит за счет прибавления энергии в струи, а не только за счет распределения энергий, о чем говорят уравнения Бернулли. При этом сам факт сжатия тела газового вихря свидетельствует о том, что и плотность стенок вихря имеет высокие значения, а температура стенок понижается. Это говорит о том, что к поступательной скорости внутренних слоев вихря, за счет действия внешнего давления, происходит добавление скорости, связанной с перераспределением тепловой энергии в энергию поступательного движения. Поэтому тангенциальная скорость движения внутренних слоев будет иметь большее значение, чем это показано с формулы.

К сожалению, механизм действия тепловой энергии в хаотичном движении молекул газа в поступательном движении потоков газового вихря рассмотрен в газовой динамике не в полной мере. Исходя из сложности поставленной задачи, в данном случае о нем можно говорить только предположительно, опираясь на тот факт, что газ в стенках вихря имеет высокую плотность и пониженную относительно внешней среды температуру.

Установлено что тепловая энергия может передаваться внутренними слоями газа по нескольким направлениям – во внешнюю среду и в ускоряющиеся потоки тела вихря.

Отдача тепла во внешнюю среду производится при участии центробежной силы молекул, которая обладает скоростными характеристиками, и выполняет данное действие по направлению от внутренних слоев к внешним слоям (по принципу испарения жидкости с поверхности). Оставшиеся молекулы участвуют в перераспределении скорости, температура слоя же остается пониженной.

Передача тепловой энергии слоям, которые поступательно движутся, происходит за счет того, что среднее значение пробега молекулы в тангенциальном направлении увеличивается. При условии сохранения удельной энергии газа выполняется перераспределение между тангенциальной и нормальной скоростями. В этом процессе происходит увеличение упорядоченной части тангенциальной составляющей движения, что приводит к сокращению тангенциальной части хаотического движения, вследствие чего происходит общее снижение скорости теплового движения. При этом происходит снижение температуры:

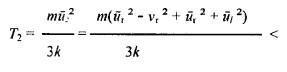
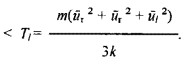
Где m – масса молекулы газа; τ – координата тангенциальной составляющей движения; координата r – радиальной; l – осевой; ū – средняя скорость хаотического (теплового) движения молекул газа; vr – скорость упорядоченного тангенциального движения (или скорость движения струи газа); к – постоянная Больцмана.

В данном случае скорость внутренних потоков газа оказывается большей, чем скорость, образующаяся в результате разгона газа внешним давлением окружающей среды, что имеет отличие данного процесса от движения твердого тела с меняющимся радиусом.

Поэтому, хотя бы на качественном уровне механизм утраты тепловой энергии внутренними слоями газового вихря становится объяснимым. Возможно в ближайшем будущем ученые уделят этому вопросу более пристальное внимание.

При сжатии тела вихря внешним давлением на его поверхности происходит равенство давлений

Pc=Pu+Pi

Где Рс – давление эфира в свободном пространстве; Рu- давление, созданное центробежной силой на поверхности вихря; Рi – давление внутри вихря. При этом соблюдается условие

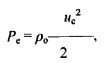
Где р0 – плотность газа в свободном пространстве, uc – средняя скорость хаотического движения молекул газа.

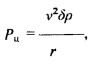
Где v – поступательная (тангенциальная) скорость движения стенки вихря; δ – толщина стенки; ρ – плотность газа в стенке вихря; r – радиус стенки вихря.

В центральной части вихря присутствует внутреннее давление Рi и плотность газа в стенке вихря, которые связанны температурным соотношением:

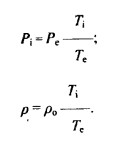
При обозначении Ti/Te=kt, получаем следующее уравнение

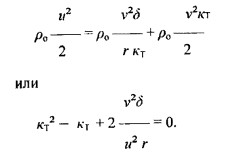
При решении данного уравнения мы получили следующее выражение

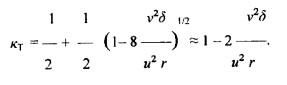
Из этого следует, что температуру внутри газового вихря и его стенке можно определить по следующей формуле

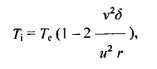
А плотность стенки газового вихря можно определить по следующей формуле

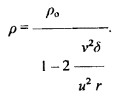
Из этих выражений становиться ясно, что по мере увеличения скорости вращения вихря температура внутренней его части снижается, а плотность стенок увеличивается.

Давайте определим скорость движения стенки вихря при его сжатии.

Прирост скоростных показаний в движении стенки происходит за счет уменьшения теплового содержания газа внутри вихря, и это видно из

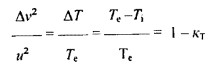
И поэтому

А в результате мы видим, что

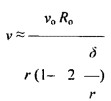
Где R0 и v0 – начальный радиус вихревого образования и соответственно начальная скорость поступательного движения газовых масс в момент формирования вихревого движения.

Поэтому, скорость потока сжимаемого газа в теле вихря может в значительной мере превышать скорость потока жидкости при одинаковых внешних показателях вихрей.

Внутри тела вихря в зоне, которая разрежена, тангенциальная скорость по направлению к центру будет постепенно убывать, что схоже с убыванием скорости во время движения вращающегося твердого тела, хотя природная составляющая данного движения носит иной характер. В отличие от жидких вихрей, в которых центр заполнен жидкостью с одинаковой плотностью, что и окраина. Некоторые физики считают, что вихри вращаются по закону твердого тела, что является ошибкой и газовый вихрь обладает трубчатой структурой. В центральной области газового вихря давление газа понижено из за разброса частиц из центральной части центробежной силой, а сам вихрь имеет оболочку из приграничного слоя, в котором низкая температура и вязкость. В таком вихре значение плотности имеет плавный переход от высоких показателей стенок к плотности газа в окружающей его среде.

Исходя из вышесказанного, можно сделать вывод, что газовый вихрь при своем формировании концентрирует в себе энергию окружающей среды и данный процесс имеет существенные отличия от любых других процессов, которые сопровождаются рассеиванием энергии в окружающем пространстве.