Как известно, элементом эфира является амер, который характеризуется единственной формой движения, а именно, равномерным поступательным движением в пространстве. Взаимодействие амеров между собой происходит путем соударения, что приводит к обмену количествами движений (импульсами). Такие соударения считаются упругими, так как они происходят практически без потери количества движения.
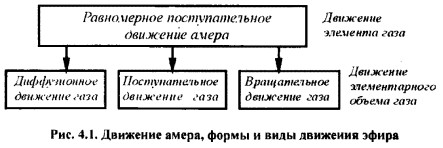
Элементарный объем эфира или совокупность амеров обладает несколькими формами движений – диффузионной, поступательной и вращательной.
Что касается диффузионной формы движения амеров, то она в эфире есть всегда, даже в состоянии его равновесия (то есть внешнее движение в эфире отсутствует). Поэтому данную форму движения амеров принято считать основной, исходной для рассмотрения любых других форм движений.
Данная форма движения эфира, как и любого газообразного вещества, может обеспечивать три вида движений: перенос плотности, перенос импульса (количества движений) и перенос энергии.
Поступательная форма движения эфира может обеспечить два вида движений: эфирный ветер (ламинарный ветер) и продольно колебательное (звук, в диапазоне модуля упругости).
Вращательное движение эфира может основываться на двух видах движений: по типу смерча (разомкнутое вращение) и по типу тороида (замкнутое вращение).
Все перечисленные виды движений могут давать различные комбинации видов движений, которые могут соответствовать тем или иным физическим взаимодействиям, физическим полям и явлениям. правда вариантность не будет сильно большой, так как в учет берутся взаимодействия потоков эфира, которые обладают разными формами и видами движений. Главное, что в основе всех видов движений лежит единственный вид движения – движение амеров в пространстве, а также единственный вид их взаимодействия – упругое соударение, что свидетельствует о том, это основа всех видов движения эфира в организации вещества, начиная с элементарных частиц и заканчивая Вселенной. Поэтому логично заявить, что следует все виды взаимодействий можно свести к механике – тому или иному виду перемещения эфирных масс в пространстве.
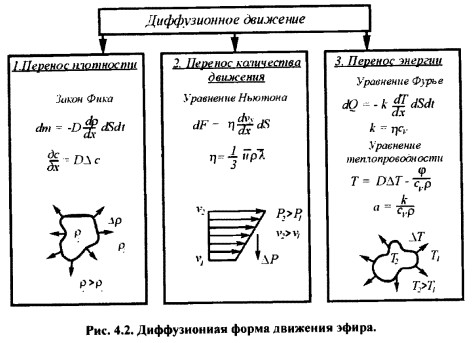
Диффузионная форма движения эфира.
1. Перенос плотности. Переносное явление в диффузионном движении присутствует в любом газообразном веществе, как в равномерном распределении, так и в неравномерном распределении плотности. Свойство переносного движения – это выравнивание концентрации плотности и концентрации масс (самодиффузии), в случае, если имеется отсутствие восстанавливающего неравновесного состояния причин.
Для переносного диффузионного движения свойственны определенные особенности, которые связаны с тем, что в однокомпонентной среде (эфире) на процесс самодиффузии может накладываться термодиффузия. Мы не можем также утверждать точно, что эфир – это однокомпонентная система, а амеры одинаковы между собой. Вернее будет сказать, что амеры являются вихревыми образованиями (эфира-2) и имеют различия, а также могут формировать сложные структурные элементы типа молекул. Это правда тоже нельзя утверждать с точностью, так как рассмотрение вопроса о тонкой структуре эфира, реальных формах амер, видах скоростных характеристик, особенностях взаимодействий и т.д., необходимо отложить на будущее.
Явление диффузии плотности можно рассматривать через первый закон Фика:
dM=-D dSdt dpэ/dx
Где dM – это масса, которая переносится во времени dt через площадку dS по направлению к нормали x, которая направлена к рассматриваемой площадке по убыванию плотности; D – коэффициент самодиффузии; dpэ/dx – градиент плотности.
В том случае, когда происходит трехмерная диффузия, изменение концентрации с течением времени при постоянном температурном режиме при отсутствии внешних сил можно сформулировать при помощи уравнения самодиффузии:
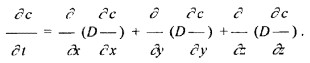
Если D не имеет зависимости от концентрации, то уравнение можно представить в виде выражения:
c/dt=DΔc – второй закон Фика. В котором Δ – дифференциальный оператор Лапласа, с – концентрация частиц газового вещества.
2. Перенос импульса. Перенос количества движения, который современные физики называют неправильно импульсом (так как физический импульс – это произведение количества сил на время действия, что не наблюдается в отдельных элементарных частицах, для которых характерны масса и скорость движения), что реализуется в слоях среды, которые могут двигаться относительно друг друга. Перенос энергии с одного слоя в другой обусловлено причиной вязкости трения или вязкого состояния газа.
Перенос количественных показателей движения можно охарактеризовать уравнением Ньютона, которое создано для движения вязких жидкостей:
dFx=ηdSdv1/dx
где dF – это силовая характеристика трения, которая действует на площадку dS поверхности слоя вдоль плоскости поверхности, dv1/dx – это соотношение скоростных характеристик движения слоев в направлении оси у, которая перпендикульярна поверхности слоя; η – коэффициент внутреннего трения, который приравнивается к силе трения между слоями с площадью, равной одной единицы, при градиенте скорости, равной 1.
Элементарная кинетическая теория:
η=uλρ√3
При более точной формулировке множитель можно заменить с 1/3 на коэффициент ϕ, который зависит от характера взаимодействия молекул. Так для молекул, которые сталкиваются гладкие твёрдые сферы, ϕ=0,499. Если рассматривать более точные модели сил взаимодействия, то значение ϕ можно рассматривать как функцию температуры, которая возрастает. На данном этапе становления эфиродинамики подымать вопрос развития данной функции является нецелесообразным.
Коэффициенты перекоса к и η не могут зависеть от плотности газа, так как произведение λρ не имеет зависимости от ρ. Вязкость газа возрастает при повышении температуры в пропорциональном соотношении относительно Т.
3. Перенос энергии. Если существуют в газе области с различными среднестатистическими скоростями частиц при различных температурах. В таком состоянии возникает термодиффузия, при которой температуры могут выравниваться, если не происходит непрерывное рассеивание тепла в пространстве и в том случае, если к данным областям нет подвода тепла извне. В противоположном случае есть необходимость установления некоторого градиента температур.
Перенос тепла через единицу поверхности можно определить при помощи уравнения Фурье:
dQ=-kdSdtdT/dx
где к=ηct – коэффициент теплопроводности, который приравнивается к количеству теплоты, которая переносится через единицу поверхности за определенную величину времени при градиенте температуры, что равен единице; dT/dx – это градиент температуры.
Разность слоев пограничного слоя можно определить при помощи выражения:
ΔТ=(Δu)2/2cρ
Где Δu – перепад скоростей слоев; cρ – это теплоемкость газа при неизменном давлении.
Взаимосвязь между динамической вязкостью и температурой в пограничном слое можно выразить следующей формулой:
η/η0=(T/T0)ξ, 0,5 ≤ ξ ≤ 1
Поэтому принято считать, что в пограничном слое, в котором имеет место существенный градиент скоростей, температурный показатель и вязкость газа снижены. Это и объясняет стабильность вихревых образований в эфире.
Уравнение распространения тепла в эфире, как и в любой газообразной среде, можно записать при помощи следующего выражения:
Tt=αΔT-∫cvρ, α=kt/cvρэ
Где Т(Ь=М,t) – температура в точке М (x, y, z) в момент времени t; kt – коэффициент теплопроводности, который является постоянной величиной, α – это коэффициент температуропроводности; ƒ- это плотность тепловых источников.
Поступательная форма движения эфира.
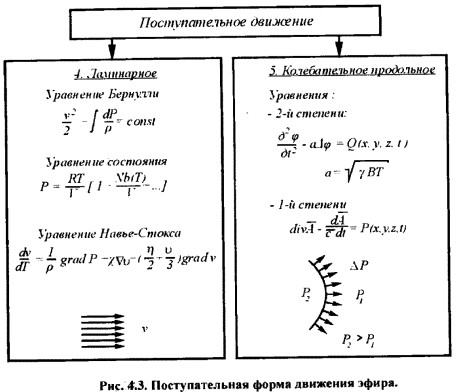
1. Ламинарное течение эфира. Ламинарное течение газообразного вещества может возникать в присутствии разности давлений в двух областях пространства. При движении газа поступательно диффузионное движение сохраняется, но при хаотическом движении молекул происходит наложение упорядоченного движения молекул в общем направлении. Вращательное движение в объеме газообразного вещества отсутствует. При поступательном движении может происходить деформация объемов.
При помощи математических выражений, которые описывают поступательное движение эфира при ламинарном течении, можно описать сжимаемые вязкие газы (уравнения гидромеханики):
Уравнение Бернулли, описывает сохранение энергии в струе газа (сумма кинетической и потенциальной энергий в струе газа может сохраняться независимо от сечения газовой струи):
V2/2+∫dP/ρ=const;
Уравнение состояния:
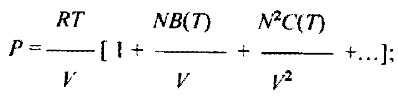
Уравнение Навье-Стокса:
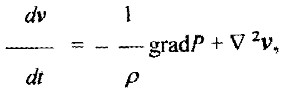
Также можно использовать в описании движения газа пограничных слоях интегральные соотношения Кармана и многие другие.
При использовании уравнений гидромеханики по отношению к эфиру следует учесть отсутствие объемных сил при начальном этапе исследований, при котором фактором существования эфира-2 пренебрегают. В других частных случаях можно использовать упрощенные уравнения, например уравнения Эйлера вместо уравнений Навье-Стокса.
Упрощение уравнений предоставляет возможность пренебречь вязкостью и сжимаемостью, но только в тех случаях, когда не происходит искажение исходной модели явления.
В некоторых направлениях, например, в электродинамике, вывод уравнений, которые базируются на несжимаемости эфира и отсутствии вязкости, в данный период не представляет возможности данными параметрами пренебрегать, так как исследования подтвердили их существенность для большинства частных явлений.
2. Продольное колебательное движение в газе. Данное явление может возникнуть при появлении малого избыточного давления. Скорость распространения данного избыточного давления в пределах модуля упругости можно назвать скоростью распространения звука.
Описать продольное колебание в среде можно при помощи волнового уравнения второго порядка:
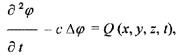
Где Q (x, y, z, t) – это возмущающейся воздействие; ϕ – скалярный потенциал; с – это скорость распространения продольного возмущения или скорость звука, которую можно определить при помощи следующего выражения:
c=√ϒP/ρ
где ϒ – показатель адиабаты, Р – это давление, а ρ – это плотность газа.
Также существует волновые уравнения первого порядка, которые существенно отличаются от волновых уравнений второго порядка (своей простотой). Также их отличие в том, что в них нет искусственных приемов для ликвидации донного из решений, которое дает расхождения в выражении. Для одномерного колебания лучше всего подходит выражение
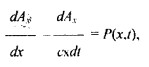
Для трехмерного:
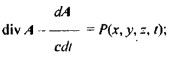
Допустимо деление на вектор, так как данный вектор совпадает по направлению с вектором А, который находится в числителе.
Вращательная форма движения эфира.
1. Разомкнутое вращательное движение может проявляться в турбулентностях и сформировавшихся вихрях. Во время вращательного движения ось вихря устремляется к бесконечности, а скорость вращения уменьшается при постепенном удалении от оси.
Определенных случаях сжимаемостью эфира можно пренебречь, например, в свободном от вещества пространстве и это описывается в уравнении вращательного вихревого движения вязкой несжимаемой жидкости:
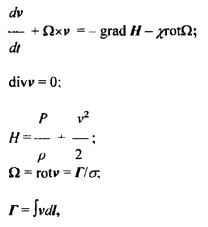
Где v – средняя поступательная скорость частиц в определенной точке пространства; Г – интенсивность вихря; σ – площадь вихря.
При описании структуры вещества нельзя пренебрегать сжимаемостью вихря, так как данный показатель является определяющим при объяснении поведения эфира. В таком случае уравнения принимают более сложную форму.

2. Замкнутое вращательное движение – это тороидальное движение газа. Для описания данного явления можно использовать закон Био-Савара (в случае, когда вязкостью и сжимаемостью газа можно пренебречь):
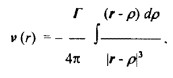
Где ρ – это радиус-вектор.
Замкнутое вращательное движение эфира можно считать основой структур различных материальных образований на уровне образования материи элементарными частицами.
Элементарный объем эфира или совокупность амеров обладает несколькими формами движений – диффузионной, поступательной и вращательной.
Что касается диффузионной формы движения амеров, то она в эфире есть всегда, даже в состоянии его равновесия (то есть внешнее движение в эфире отсутствует). Поэтому данную форму движения амеров принято считать основной, исходной для рассмотрения любых других форм движений.

Данная форма движения эфира, как и любого газообразного вещества, может обеспечивать три вида движений: перенос плотности, перенос импульса (количества движений) и перенос энергии.
Поступательная форма движения эфира может обеспечить два вида движений: эфирный ветер (ламинарный ветер) и продольно колебательное (звук, в диапазоне модуля упругости).
Вращательное движение эфира может основываться на двух видах движений: по типу смерча (разомкнутое вращение) и по типу тороида (замкнутое вращение).
Все перечисленные виды движений могут давать различные комбинации видов движений, которые могут соответствовать тем или иным физическим взаимодействиям, физическим полям и явлениям. правда вариантность не будет сильно большой, так как в учет берутся взаимодействия потоков эфира, которые обладают разными формами и видами движений. Главное, что в основе всех видов движений лежит единственный вид движения – движение амеров в пространстве, а также единственный вид их взаимодействия – упругое соударение, что свидетельствует о том, это основа всех видов движения эфира в организации вещества, начиная с элементарных частиц и заканчивая Вселенной. Поэтому логично заявить, что следует все виды взаимодействий можно свести к механике – тому или иному виду перемещения эфирных масс в пространстве.
Диффузионная форма движения эфира.
1. Перенос плотности. Переносное явление в диффузионном движении присутствует в любом газообразном веществе, как в равномерном распределении, так и в неравномерном распределении плотности. Свойство переносного движения – это выравнивание концентрации плотности и концентрации масс (самодиффузии), в случае, если имеется отсутствие восстанавливающего неравновесного состояния причин.

Для переносного диффузионного движения свойственны определенные особенности, которые связаны с тем, что в однокомпонентной среде (эфире) на процесс самодиффузии может накладываться термодиффузия. Мы не можем также утверждать точно, что эфир – это однокомпонентная система, а амеры одинаковы между собой. Вернее будет сказать, что амеры являются вихревыми образованиями (эфира-2) и имеют различия, а также могут формировать сложные структурные элементы типа молекул. Это правда тоже нельзя утверждать с точностью, так как рассмотрение вопроса о тонкой структуре эфира, реальных формах амер, видах скоростных характеристик, особенностях взаимодействий и т.д., необходимо отложить на будущее.
Явление диффузии плотности можно рассматривать через первый закон Фика:
dM=-D dSdt dpэ/dx
Где dM – это масса, которая переносится во времени dt через площадку dS по направлению к нормали x, которая направлена к рассматриваемой площадке по убыванию плотности; D – коэффициент самодиффузии; dpэ/dx – градиент плотности.
В том случае, когда происходит трехмерная диффузия, изменение концентрации с течением времени при постоянном температурном режиме при отсутствии внешних сил можно сформулировать при помощи уравнения самодиффузии:
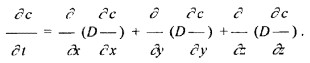
Если D не имеет зависимости от концентрации, то уравнение можно представить в виде выражения:
c/dt=DΔc – второй закон Фика. В котором Δ – дифференциальный оператор Лапласа, с – концентрация частиц газового вещества.
2. Перенос импульса. Перенос количества движения, который современные физики называют неправильно импульсом (так как физический импульс – это произведение количества сил на время действия, что не наблюдается в отдельных элементарных частицах, для которых характерны масса и скорость движения), что реализуется в слоях среды, которые могут двигаться относительно друг друга. Перенос энергии с одного слоя в другой обусловлено причиной вязкости трения или вязкого состояния газа.
Перенос количественных показателей движения можно охарактеризовать уравнением Ньютона, которое создано для движения вязких жидкостей:
dFx=ηdSdv1/dx
где dF – это силовая характеристика трения, которая действует на площадку dS поверхности слоя вдоль плоскости поверхности, dv1/dx – это соотношение скоростных характеристик движения слоев в направлении оси у, которая перпендикульярна поверхности слоя; η – коэффициент внутреннего трения, который приравнивается к силе трения между слоями с площадью, равной одной единицы, при градиенте скорости, равной 1.
Элементарная кинетическая теория:
η=uλρ√3
При более точной формулировке множитель можно заменить с 1/3 на коэффициент ϕ, который зависит от характера взаимодействия молекул. Так для молекул, которые сталкиваются гладкие твёрдые сферы, ϕ=0,499. Если рассматривать более точные модели сил взаимодействия, то значение ϕ можно рассматривать как функцию температуры, которая возрастает. На данном этапе становления эфиродинамики подымать вопрос развития данной функции является нецелесообразным.
Коэффициенты перекоса к и η не могут зависеть от плотности газа, так как произведение λρ не имеет зависимости от ρ. Вязкость газа возрастает при повышении температуры в пропорциональном соотношении относительно Т.
3. Перенос энергии. Если существуют в газе области с различными среднестатистическими скоростями частиц при различных температурах. В таком состоянии возникает термодиффузия, при которой температуры могут выравниваться, если не происходит непрерывное рассеивание тепла в пространстве и в том случае, если к данным областям нет подвода тепла извне. В противоположном случае есть необходимость установления некоторого градиента температур.
Перенос тепла через единицу поверхности можно определить при помощи уравнения Фурье:
dQ=-kdSdtdT/dx
где к=ηct – коэффициент теплопроводности, который приравнивается к количеству теплоты, которая переносится через единицу поверхности за определенную величину времени при градиенте температуры, что равен единице; dT/dx – это градиент температуры.
Разность слоев пограничного слоя можно определить при помощи выражения:
ΔТ=(Δu)2/2cρ
Где Δu – перепад скоростей слоев; cρ – это теплоемкость газа при неизменном давлении.
Взаимосвязь между динамической вязкостью и температурой в пограничном слое можно выразить следующей формулой:
η/η0=(T/T0)ξ, 0,5 ≤ ξ ≤ 1
Поэтому принято считать, что в пограничном слое, в котором имеет место существенный градиент скоростей, температурный показатель и вязкость газа снижены. Это и объясняет стабильность вихревых образований в эфире.
Уравнение распространения тепла в эфире, как и в любой газообразной среде, можно записать при помощи следующего выражения:
Tt=αΔT-∫cvρ, α=kt/cvρэ
Где Т(Ь=М,t) – температура в точке М (x, y, z) в момент времени t; kt – коэффициент теплопроводности, который является постоянной величиной, α – это коэффициент температуропроводности; ƒ- это плотность тепловых источников.
Поступательная форма движения эфира.
1. Ламинарное течение эфира. Ламинарное течение газообразного вещества может возникать в присутствии разности давлений в двух областях пространства. При движении газа поступательно диффузионное движение сохраняется, но при хаотическом движении молекул происходит наложение упорядоченного движения молекул в общем направлении. Вращательное движение в объеме газообразного вещества отсутствует. При поступательном движении может происходить деформация объемов.
При помощи математических выражений, которые описывают поступательное движение эфира при ламинарном течении, можно описать сжимаемые вязкие газы (уравнения гидромеханики):
Уравнение Бернулли, описывает сохранение энергии в струе газа (сумма кинетической и потенциальной энергий в струе газа может сохраняться независимо от сечения газовой струи):
V2/2+∫dP/ρ=const;
Уравнение состояния:
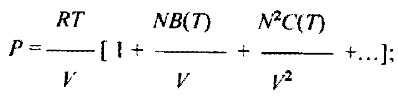
Уравнение Навье-Стокса:
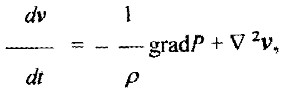
Также можно использовать в описании движения газа пограничных слоях интегральные соотношения Кармана и многие другие.

При использовании уравнений гидромеханики по отношению к эфиру следует учесть отсутствие объемных сил при начальном этапе исследований, при котором фактором существования эфира-2 пренебрегают. В других частных случаях можно использовать упрощенные уравнения, например уравнения Эйлера вместо уравнений Навье-Стокса.
Упрощение уравнений предоставляет возможность пренебречь вязкостью и сжимаемостью, но только в тех случаях, когда не происходит искажение исходной модели явления.
В некоторых направлениях, например, в электродинамике, вывод уравнений, которые базируются на несжимаемости эфира и отсутствии вязкости, в данный период не представляет возможности данными параметрами пренебрегать, так как исследования подтвердили их существенность для большинства частных явлений.
2. Продольное колебательное движение в газе. Данное явление может возникнуть при появлении малого избыточного давления. Скорость распространения данного избыточного давления в пределах модуля упругости можно назвать скоростью распространения звука.
Описать продольное колебание в среде можно при помощи волнового уравнения второго порядка:
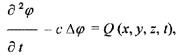
Где Q (x, y, z, t) – это возмущающейся воздействие; ϕ – скалярный потенциал; с – это скорость распространения продольного возмущения или скорость звука, которую можно определить при помощи следующего выражения:
c=√ϒP/ρ
где ϒ – показатель адиабаты, Р – это давление, а ρ – это плотность газа.
Также существует волновые уравнения первого порядка, которые существенно отличаются от волновых уравнений второго порядка (своей простотой). Также их отличие в том, что в них нет искусственных приемов для ликвидации донного из решений, которое дает расхождения в выражении. Для одномерного колебания лучше всего подходит выражение
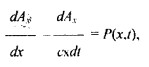
Для трехмерного:
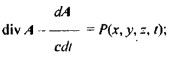
Допустимо деление на вектор, так как данный вектор совпадает по направлению с вектором А, который находится в числителе.
Вращательная форма движения эфира.
1. Разомкнутое вращательное движение может проявляться в турбулентностях и сформировавшихся вихрях. Во время вращательного движения ось вихря устремляется к бесконечности, а скорость вращения уменьшается при постепенном удалении от оси.
Определенных случаях сжимаемостью эфира можно пренебречь, например, в свободном от вещества пространстве и это описывается в уравнении вращательного вихревого движения вязкой несжимаемой жидкости:
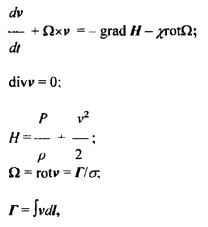
Где v – средняя поступательная скорость частиц в определенной точке пространства; Г – интенсивность вихря; σ – площадь вихря.
При описании структуры вещества нельзя пренебрегать сжимаемостью вихря, так как данный показатель является определяющим при объяснении поведения эфира. В таком случае уравнения принимают более сложную форму.

2. Замкнутое вращательное движение – это тороидальное движение газа. Для описания данного явления можно использовать закон Био-Савара (в случае, когда вязкостью и сжимаемостью газа можно пренебречь):
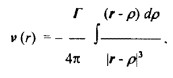
Где ρ – это радиус-вектор.
Замкнутое вращательное движение эфира можно считать основой структур различных материальных образований на уровне образования материи элементарными частицами.





