В чём заключается разница между специальной теорией относительности и механики Ньютона. В законах специальной теории относительности берётся во внимание скорость распространения силового взаимодействия в электромагнитном и гравитационном поле, а в законах Ньютона приоритет отдаётся принципу «дальнодействия», то есть силовое взаимодействие происходит моментально.
В 1835 году Гаусс сделал следующий вывод силового взаимодействия электрических зарядов в электрических и магнитных полях:
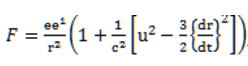
,
где F – это сила взаимодействия между частицами с электромагнитными зарядами e и e1, которые совершают движение с относительной скоростью u; r – это расстояние между движущимися частицами;dr/dt – это абсолютная скорость вдоль линий, с – скорость света.
Данная формула была продемонстрирована ученику Гаусса – Веберу. Только в 1867 году Вебер обнародовал данную формулу – после смерти своего учителя.
Мы же запишем данный закон в такой форме:
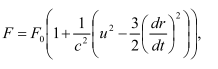
Где примем F0 за силу взаимодействий частиц при относительной скорости u=0.
Теперь осталось проанализировать данный закон. Если взять вектор относительной скорости u за разность векторов скоростей обоих частиц, то закон даёт правильное решение в обобщённом виде, так вектор u перпендикулярен линии, которая соединяет центры частиц, то есть мы имеем dr/dt=0. Из этого следует, что:

Теперь остаётся сравнить выражение релятивисткой динамики:
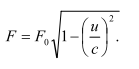
Коэффициент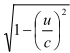
необходимо разложить за степенями u/c, что даёт следующее:

Это выражение говорит о том, что коэффициент уменьшения эффективности действия электрического поля со скоростью по закону Гаусса в точности с первыми числами имеет отношение к релятивистскому коэффициенту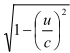
по степеням. Уже в 1835 году Гаусс вплотную приблизился к открытию уравнения динамики движущихся частиц в электрическом поле на больших скоростях. Свой закон Гаусс вывел из закона механики Ньютона с учётом запаздывания потенциалов, то есть он учитывал скорость распространения силового взаимодействия в силовом поле.
Мы видим, что силовое взаимодействие в электрическом поле распространяется со световой скоростью вследствие деформации в поле частиц. Такая деформация не может происходить мгновенно. Об этом говорил В. Ритц: «взаимодействие не может быть мгновенным». Если частица может перемещаться, то в ходе её движения перемещается и деформация самого поля. Силовое взаимодействие распространяется со скоростью света, так как частицы выполняют движение со скоростью «с» относительно источника поля, то есть сила не воздействует на саму частицу. Если частица движется с меньшей скоростью, то поле может воздействовать на неё с эффективностью, которая имеет прямую зависимость от скорости движения деформационного поля.
Вывод: нелинейное уменьшение эффективности действия электрических или магнитных полей при релятивистских скоростях является результатом конечной скорости распространения силового взаимодействия, которое описано законами механики Ньютона. При этом не происходит изменение скорости времени и изменения пространственных масштабов.
Уравнение релятивистской динамики основано на законе силового взаимодействия электрического, магнитного и электромагнитного полей на различные материальные объекты на основе законов механики Ньютона.
В 1835 году Гаусс сделал следующий вывод силового взаимодействия электрических зарядов в электрических и магнитных полях:
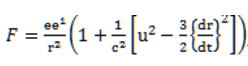
,
где F – это сила взаимодействия между частицами с электромагнитными зарядами e и e1, которые совершают движение с относительной скоростью u; r – это расстояние между движущимися частицами;dr/dt – это абсолютная скорость вдоль линий, с – скорость света.
Данная формула была продемонстрирована ученику Гаусса – Веберу. Только в 1867 году Вебер обнародовал данную формулу – после смерти своего учителя.
Мы же запишем данный закон в такой форме:
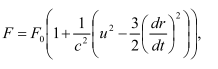
Где примем F0 за силу взаимодействий частиц при относительной скорости u=0.
Теперь осталось проанализировать данный закон. Если взять вектор относительной скорости u за разность векторов скоростей обоих частиц, то закон даёт правильное решение в обобщённом виде, так вектор u перпендикулярен линии, которая соединяет центры частиц, то есть мы имеем dr/dt=0. Из этого следует, что:

Теперь остаётся сравнить выражение релятивисткой динамики:
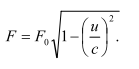
Коэффициент
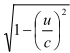
необходимо разложить за степенями u/c, что даёт следующее:

Это выражение говорит о том, что коэффициент уменьшения эффективности действия электрического поля со скоростью по закону Гаусса в точности с первыми числами имеет отношение к релятивистскому коэффициенту
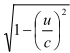
по степеням. Уже в 1835 году Гаусс вплотную приблизился к открытию уравнения динамики движущихся частиц в электрическом поле на больших скоростях. Свой закон Гаусс вывел из закона механики Ньютона с учётом запаздывания потенциалов, то есть он учитывал скорость распространения силового взаимодействия в силовом поле.
Мы видим, что силовое взаимодействие в электрическом поле распространяется со световой скоростью вследствие деформации в поле частиц. Такая деформация не может происходить мгновенно. Об этом говорил В. Ритц: «взаимодействие не может быть мгновенным». Если частица может перемещаться, то в ходе её движения перемещается и деформация самого поля. Силовое взаимодействие распространяется со скоростью света, так как частицы выполняют движение со скоростью «с» относительно источника поля, то есть сила не воздействует на саму частицу. Если частица движется с меньшей скоростью, то поле может воздействовать на неё с эффективностью, которая имеет прямую зависимость от скорости движения деформационного поля.
Вывод: нелинейное уменьшение эффективности действия электрических или магнитных полей при релятивистских скоростях является результатом конечной скорости распространения силового взаимодействия, которое описано законами механики Ньютона. При этом не происходит изменение скорости времени и изменения пространственных масштабов.
Уравнение релятивистской динамики основано на законе силового взаимодействия электрического, магнитного и электромагнитного полей на различные материальные объекты на основе законов механики Ньютона.





