В данный момент мы полностью готовы окунуться в исследования преобразований Лоренца, которые изменяют основные законы механики. До недавнего времени ученные могли объяснить такие физические понятия, как длина и время, но им не удавалось изменить данную формулу (1).

В данной статье мы попробуем это сделать и изучить следствия формулы Эйнштейна для массы в механике Ньютона. Наш путь мы открываем с закона силы. Как гласит закон – сила является ничто иное, как быстрота изменения импульса:

Где импульс представляет выражение mv, но теперь мы видим, что:

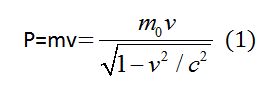
Так выглядит закон Ньютона в записи Эйнштейна. В данном законе привычно равенство действия и противодействия (конечно, не на всех отрезках, но при нахождении среднего показателя времени, это действительно так). В формуле (1), где присуща переменная масса (новая m), импульс должен сохраняться.

Давайте исследуем, как импульс может зависеть от скорости. Ньютон в своей механике показал, что импульс пропорционален скорости. В релятивистской механике на больших интервалах скоростей имеется множество малых (с), которые приблизительно пропорциональны (см. (1)), так как корень приближен к единице. Но если v≂c, то значение корня приблизилось к нулю и значение импульса безгранично растет.

Многие из вас спросят, что будет, если к телу приложить постоянную силу? Если следовать законам Ньютоновской механики, скорость тела будет непрерывно расти и сможет обогнать скорость света. Если же смотреть на данный вопрос со стороны релятивистской механики, то такое считается невозможным. По теории относительности скорость тела не растет, а возрастает импульс, а также возрастает масса тела. По прохождению определенного времени скорость прекращает изменяться, но импульс растет дальше. Так сила не приводит к существенным изменениям в показаниях скорости тела, то принято считать, что тело обладает огромной инерцией. Такое подтверждение показывает релятивистская формула (1), которая связана с массой тела. Данная формулировка утверждает, что инерция имеет огромную величину при условии, когда v приблизительно равна с.

Давайте рассмотрим пример на практике. Для того, чтобы произвести отклонение быстрых электронов в синхротроне Калифорнийского Технологического института, понадобилось создание магнитного поля, которое 2000 раз сильнее, чем предусмотрено в законах Ньютона. Если говорить простым языком, то понадобилось получение массы электронов в синхротроне, которая в 2000 раз больше, чем их нормальная масса. Это говорит, что электроны достигают массы протона! Если показатель т больше в 2000 от m0, то 1-v2/c2 будет равно 1/4 000000. Это свидетельствует о том, что скорость электронов достигает отметки скорости света. Давайте представим такую ситуацию – марафон, где участвуют свет и электроны, которые должны преодолеть расстояние в 200 метров. Кто быстрее доберется до финиша? Конечно свет, так как он имеет большую скорость. Но если присмотреться к показаниям фотофиниша, то можно увидеть, что электроны отстали от света на 1/30 мм (!). То есть данное расстояние можно сравнить с толщиной одного листа бумаги! Мы имеем электрон с огромной массой, который имеет скорость не выше скорости света.

Но к чему приведет релятивистский рост массы? Давайте поэкспериментируем с движением молекул газа в баллоне. При нагревании газа, молекулы начинают активно двигаться и увеличивать скорость. При этом растет их масса. Газ наберет в массе. А насколько увеличится масса?

Давайте разложим m0/√(1-v2/c2)=m0(1- v2/c2)-1/2 , используя формулу бинома Ньютона. Это поможет нам определить приблизительный рост массы при маленьких скоростях. Тогда мы получим,

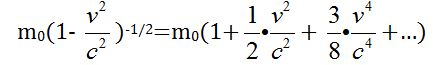
из данной формулы мы видим, что при малом значении (v) ряд сходится и первых двух-трех показателей достаточно для расчета. Поэтому можно составить следующую формулу:

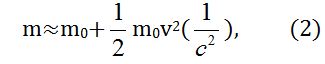
где мы видим, что второй член отвечает за рост массы при повышении скорости. Если увеличивается температура, то и растет v2 в равной мере. То есть масса растет прямопропорционально температуре. Но здесь присущ старомодный ньютоновский закон кинетической энергии

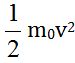
Это позволяет утверждать о росте массы равной росту кинетической энергии, которая делится на c2. Тогда мы получаем △m=△(к.э.)/с2.